Points: Basic Programming Concepts

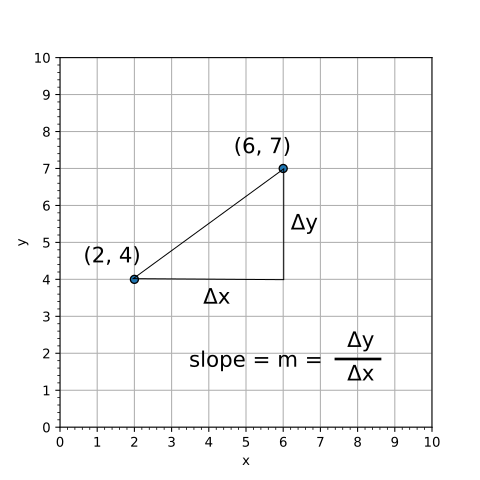
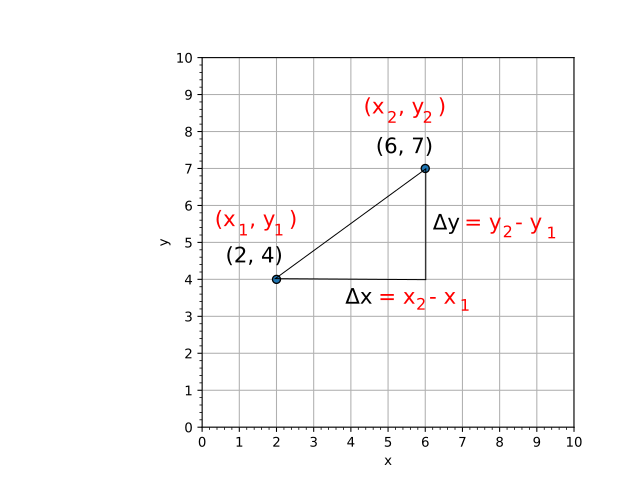
The slope (m) of a line between two points is a measure of how fast the line goes up, so you take the vertical change (the change in y (Δy)), divided by the horizantal change (the change in x (Δx). $$ m = \frac{\Delta y}{\Delta x} $$

For this specific problem we can easily calculate the change in y and change in x, however, for a program we'll want to generalize as much as possible, so we'll label the two points as Point 1 and Point 2 and the coordinates as (x₁, y₁) and (x₂, y₂):

So, ultimately, we'll go with the three equations: $$ \Delta x = x_2 - x_1 $$ $$ \Delta y = y_2 - y_1 $$ $$ m = \frac{\Delta y}{\Delta x} $$

              # First Point
              x1 = 2
              y1 = 4

              # Second Point
              x2 = 6
              y2 = 7Another, much more powerful, way of grouping things is a class. A point on the coordinate plane, with its x and y values would make a good class.

              # Vertical and Horizontal differences
              Dx = x2 - x1
              Dy = y2 - y1

              # Calculate Slope
              m = Dy / Dx

              # Print result
              print(f'The slope is {m}')

            

Comments: Anything after a "#" is commented out, which means it is ignored when the program is run. This is a good way to make notes to explain what the program is doing.

Declaring Variables: On Line 2 we create a variable named x1 and give it a value of 2. Variable names have to start with a letter, but can be upper or lower case.

Using Variables: On Line 10 we calculate the horizontal distance between the two points (Δx). I name the variable Dx instead of Δx simply because the upper case "D" is easier to type on my keyboard: Δx would work as a variable name in python.

              # First Point
              (x1, y1) =  (2, 4)

              # Second Point
              (x2, y2) = (6, 7)

              # Vertical and Horizontal differences
              Dx = x2 - x1
              Dy = y2 - y1

              # Calculate Slope
              m = Dy / Dx

              # Print result
              print(f'The slope is {m}')

            

Tuple: Line 2 makes a tuple of (2, 4) and assigns it to another tuple (x1, y1). Since there's a pair of values in each tuple, the values are assigned to their respective variables.

              class point:
                  def __init__(self, x, y):
                      self.x = x
                      self.y = y

              # First Point
              p1 =  point(2, 4)

              # Second Point
              p2 = point(6, 7)

              # Vertical and Horizontal differences
              Dx = p2.x - p1.x
              Dy = p2.y - p1.y

              # Calculate Slope
              m = Dy / Dx

              # Print result
              print(f'The slope is {m}')

            

Defining the Class: Line 1 creates a class named point.

Initialization function: Line 2's "__init__" is the class' initialization function. Your class will almost always need one of these. This one takes three variables, and the first one self is required for the class to be able to save things for later; the other two variables are just the x and y coordinates of the point.

Saving Properties: Lines 3 and 4 save the x and y values internally so we can use them later. These internal variables are specific to each time we use the class, and are called properties.

Creating Instances of the class: On Lines 7 and 10 we create our points (p1 and p2) as instances of the point class. Notice that we give each point its x and y values.

Using the Instances of the class: On Line 13 we get the horizontal difference by subtracting point 2's x value (p2.x) from point 1's (p1.x).

              # Function to find the slope
              def slope(x_1, y_1, x_2, y_2):
                  # Get vertical and Horizontal differences
                  Dx = x_2 - x_1
                  Dy = y_2 - y_1
                  # Calculate Slope
                  s = Dy / Dx
                  # Return result to main program
                  return s


              # MAIN PROGRAM STARTS HERE

              # First Point
              x1 = 2
              y1 = 4

              # Second Point
              x2 = 6
              y2 = 7

              # Use function to get the slope
              m = slope(x1, y1, x2, y2)

              # Print result
              print(f'The slope is {m}')

            

Creating the function:

                def slope(x_1, y_1, x_2, y_2):
              

Functions are created with the def keyword. In this case, the function is named slope and takes four values as inputs, which are given variable names: x_1, y_1, x_2, y_2. The function is the first thing in the code because when the program is run, it is saved so we can use it later. If a function is called before it is defined you'll get an error.

Local variables: The variable names from the function definition only exist within the function, this way multiple functions, or even the main program, can use the same variable names without conflicting with one another. Therefore, we could have used x1, y1, x2, y2 even though these names are used in the main code.

Returning the Result:

                    return s
              

On Line 9 we use the return keyword to return the result of the function to the place where it was called.

Calling the function

              m = slope(x1, y1, x2, y2)
              

We call the function by using its name (slope) and passing it the four values the function expects. We could have just put in the numbers directly, and left out Lines 14-20 like so:

              m = slope(2, 4, 6, 7)