Volumes of Revolutions-Disk Method

To solidify my knowledge of the disk method in calculus, I created a visual representation of the method, explaining it.

The Disk method is used to find the volume of shapes made by rotating a function around the x or y axis. After rotating the object to make a shape, divide the shape into multiple disks. Then find the volume of each disk, using the volume of a cylinder equation, V=πr^2h. r= function, h=the width of the disks. After finding the volumes of the individual disks, the sum of them is found to get the entire volume of the shape. As the h, or the width of the disk, goes to infinity, use the equation, V= 2πr^2dx. To find the sum of the volumes of the disks as h goes to infinity, use the equation, V=∫2πr^2dx. The following picture and presentation demonstrate this.

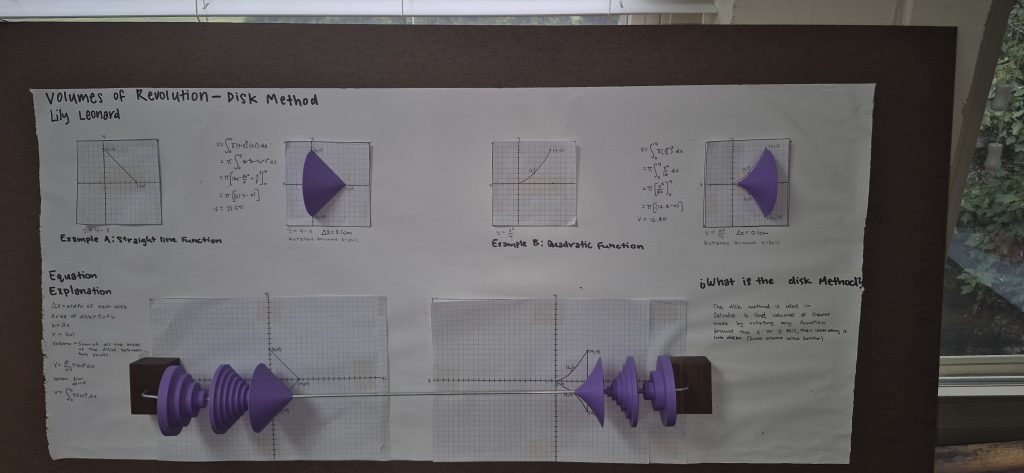
The process of making the presentation started with learning the concept and doing practice problems. I then mapped out how the presentation was going to look. Then I made the 3D shapes on OpenScad and printed them out. I used two different functions to show this concept. One linear, y= 4-x, and one quadratic, y= (x^2)/4.

I put the 3D shapes on a rod so they can slide across the graphs to demonstrate the different widths of Δx. For aesthetic purposes, I anchored the rod in wood blocks that I oiled, so they are pretty now.

$latex \int{x}$